Class 4: The Scientific Stack - Part I: numpy¶
Scientific Python¶
Introduction¶
The onion-like scientific stack of Python is composed of the most important packages used in the Python scientific world. Here’s a quick overview of the most important names in the stack, before we dive in deep:
IPython: A REPL, much like the command window in MATLAB. Lets you write Python on the fly, debug and check the performance of your code, and much (much!) more.
Jupyter: Notebooks designed for data exploration. Write code and see its output immediately, with useful rich text (Markdown) annotations to accompany it (just like this notebook!).
NumPy: Standard implementation of multi-dimensional arrays in Python.
pandas: Tabular data manipulation.
SciPy: Implements advanced algorithms widely used in scientific programming, including advanced linear algebra, data structures, curve fitting, signal processing, modeling and more.
matplotlib: A cornerstone for data visualization in Python.
seaborn: Smart visualizations of tabular data.
This scientific stack is one of the main reasons that empowered Python in recent years to the prominent role it has today. Throughout the course you will become familiar with all of the aforementioned tools, and more.
NumPy¶
NumPy is the de-facto implementation of arrays in Python. They’re very similar to MATLAB arrays (and to other implementations in other programming languages).
Although numpy is used extensively in the Python eco-system, it doesn’t come with the Python standard library, which means you have to install it first. Activate your environment and run pip install numpy from the command line (inside VSCode, for example). Only then you can follow the rest of the class.
import numpy as np # standard alias for numpy
l = [1, 2, 3]
array = np.array(l) # obviously same as np.array([1, 2, 3])
array
array([1, 2, 3])
The created array variable is a numpy array. Notice how numpy has to take existing data, in this case in the form of a list (l), and convert it into an array. In MATLAB everything is an array all the time so we don’t think of this conversion, but here the conversion happens explicitly when you call np.array() on some collection of data.
Let’s continue to examine the basic properties of this array:
# Check the dimensionality of the array:
print("Shape:\t", array.shape)
print("NDim:\t", array.ndim)
Shape: (3,)
NDim: 1
We’ve instantiated an array by calling the np.array() function on an iterable. This will create a one-dimensional numpy array, or vector. This is the first important difference from MATLAB. In MATLAB, all arrays are by default n-dimensional. If you write:
a = 1
a(:, :, :, :, :, 1) = 2
then you just received a 6-dimensional array. NumPy doesn’t allow that. The dimensions of an array are generally the dimensions it had when it was created. You can always use reshape(), like MATLAB, to define the exact number of dimensions you wish to have. You can also use newaxis() to add an axis, as we’ll see below. But these options still keep the number of elements in the array the same, they just re-order them.
This means that a 2x4 array can be reshaped into a 4x2 array, or a 2x2x2 one, but not 3x3x3.
The second difference is the idea of vectors.
print(f"The number of dimensions is {array.ndim}.")
print(f"The shape is {array.shape}.")
The number of dimensions is 1.
The shape is (3,).
As you see, ndim returns the number of dimensions. The shape is returned as a tuple, the length of which is the number of dimensions, while the values represent the number of elements in each dimensions. shape is very similar to the size() function of MATLAB.
Note that:
a = np.array(1) # wrong instatiation! Don't use it, instead write np.array([1])
print("Wrong instantiation results:")
print("Shape: ", a.shape)
print("NDim: ", a.ndim)
Wrong instantiation results:
Shape: ()
NDim: 0
So be mindful to pass an iterable.
Creating arrays with more than one dimension might look odd at a first glance:
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
arr_2d
array([[1, 2, 3],
[4, 5, 6]])
print(f"The number of dimensions is {arr_2d.ndim}.")
print(f"The shape is {arr_2d.shape}.")
print(f"The len of the array is {len(arr_2d)} - which corresponds to the shape of the 0th dimension.")
The number of dimensions is 2.
The shape is (2, 3).
The len of the array is 2 - which corresponds to the shape of the 0th dimension.
As we see, each list was considered a single “row” (dimension number 0) in the final array, very much like MATLAB, although the syntax can be confusing at first. Here’s another slightly confusing example:
c = np.array([[[1], [2]], [[3], [4]]])
c
array([[[1],
[2]],
[[3],
[4]]])
c.shape
(2, 2, 1)
Or, alternatively:
c2 = np.array([1, 2, 3, 4]).reshape((2, 2, 1))
c2.shape
(2, 2, 1)
Getting Help¶
NumPy has a ton of features, and to get around it we can use lookfor and the ? sign, besides the official reference on the internet:
np.lookfor("Create array")
Search results for 'create array'
---------------------------------
numpy.memmap
Create a memory-map to an array stored in a *binary* file on disk.
numpy.diagflat
Create a two-dimensional array with the flattened input as a diagonal.
numpy.fromiter
Create a new 1-dimensional array from an iterable object.
numpy.partition
Return a partitioned copy of an array.
numpy.ctypeslib.as_array
Create a numpy array from a ctypes array or POINTER.
numpy.ma.diagflat
Create a two-dimensional array with the flattened input as a diagonal.
numpy.ma.make_mask
Create a boolean mask from an array.
numpy.lib.Arrayterator
Buffered iterator for big arrays.
numpy.ctypeslib.as_ctypes
Create and return a ctypes object from a numpy array. Actually
numpy.ma.mrecords.fromarrays
Creates a mrecarray from a (flat) list of masked arrays.
numpy.ma.mvoid.__new__
Create a new masked array from scratch.
numpy.ma.MaskedArray.__new__
Create a new masked array from scratch.
numpy.ma.mrecords.fromtextfile
Creates a mrecarray from data stored in the file `filename`.
numpy.array
array(object, dtype=None, *, copy=True, order='K', subok=False, ndmin=0,
numpy.asarray
Convert the input to an array.
numpy.ndarray
ndarray(shape, dtype=float, buffer=None, offset=0,
numpy.recarray
Construct an ndarray that allows field access using attributes.
numpy.chararray
chararray(shape, itemsize=1, unicode=False, buffer=None, offset=0,
numpy.exp
Calculate the exponential of all elements in the input array.
numpy.pad
Pad an array.
numpy.asanyarray
Convert the input to an ndarray, but pass ndarray subclasses through.
numpy.cbrt
Return the cube-root of an array, element-wise.
numpy.copy
Return an array copy of the given object.
numpy.diag
Extract a diagonal or construct a diagonal array.
numpy.exp2
Calculate `2**p` for all `p` in the input array.
numpy.fmax
Element-wise maximum of array elements.
numpy.fmin
Element-wise minimum of array elements.
numpy.load
Load arrays or pickled objects from ``.npy``, ``.npz`` or pickled files.
numpy.modf
Return the fractional and integral parts of an array, element-wise.
numpy.rint
Round elements of the array to the nearest integer.
numpy.sort
Return a sorted copy of an array.
numpy.sqrt
Return the non-negative square-root of an array, element-wise.
numpy.array_equiv
Returns True if input arrays are shape consistent and all elements equal.
numpy.expm1
Calculate ``exp(x) - 1`` for all elements in the array.
numpy.isnan
Test element-wise for NaN and return result as a boolean array.
numpy.isnat
Test element-wise for NaT (not a time) and return result as a boolean array.
numpy.log10
Return the base 10 logarithm of the input array, element-wise.
numpy.log1p
Return the natural logarithm of one plus the input array, element-wise.
numpy.power
First array elements raised to powers from second array, element-wise.
numpy.ufunc
Functions that operate element by element on whole arrays.
numpy.choose
Construct an array from an index array and a set of arrays to choose from.
numpy.nditer
Efficient multi-dimensional iterator object to iterate over arrays.
numpy.maximum
Element-wise maximum of array elements.
numpy.minimum
Element-wise minimum of array elements.
numpy.swapaxes
Interchange two axes of an array.
numpy.full_like
Return a full array with the same shape and type as a given array.
numpy.ones_like
Return an array of ones with the same shape and type as a given array.
numpy.bitwise_or
Compute the bit-wise OR of two arrays element-wise.
numpy.empty_like
Return a new array with the same shape and type as a given array.
numpy.zeros_like
Return an array of zeros with the same shape and type as a given array.
numpy.asarray_chkfinite
Convert the input to an array, checking for NaNs or Infs.
numpy.bitwise_and
Compute the bit-wise AND of two arrays element-wise.
numpy.bitwise_xor
Compute the bit-wise XOR of two arrays element-wise.
numpy.float_power
First array elements raised to powers from second array, element-wise.
numpy.ma.exp
Calculate the exponential of all elements in the input array.
numpy.ma.mrecords.MaskedRecords.__new__
Create a new masked array from scratch.
numpy.diag_indices
Return the indices to access the main diagonal of an array.
numpy.nested_iters
Create nditers for use in nested loops
numpy.ma.sqrt
Return the non-negative square-root of an array, element-wise.
numpy.ma.log10
Return the base 10 logarithm of the input array, element-wise.
numpy.chararray.tolist
a.tolist()
numpy.put_along_axis
Put values into the destination array by matching 1d index and data slices.
numpy.ma.choose
Use an index array to construct a new array from a set of choices.
numpy.ma.maximum
Element-wise maximum of array elements.
numpy.ma.minimum
Element-wise minimum of array elements.
numpy.savez_compressed
Save several arrays into a single file in compressed ``.npz`` format.
numpy.matlib.rand
Return a matrix of random values with given shape.
numpy.datetime_as_string
Convert an array of datetimes into an array of strings.
numpy.ma.bitwise_or
Compute the bit-wise OR of two arrays element-wise.
numpy.ma.bitwise_and
Compute the bit-wise AND of two arrays element-wise.
numpy.ma.bitwise_xor
Compute the bit-wise XOR of two arrays element-wise.
numpy.ma.make_mask_none
Return a boolean mask of the given shape, filled with False.
numpy.ma.tests.test_subclassing.MSubArray.__new__
Create a new masked array from scratch.
numpy.core._multiarray_umath.clip
Clip (limit) the values in an array.
numpy.ma.tests.test_subclassing.SubMaskedArray.__new__
Create a new masked array from scratch.
numpy.ma.mrecords.fromrecords
Creates a MaskedRecords from a list of records.
numpy.core._multiarray_umath.empty_like
Return a new array with the same shape and type as a given array.
numpy.core._dtype._construction_repr
Creates a string repr of the dtype, excluding the 'dtype()' part
numpy.abs
Calculate the absolute value element-wise.
numpy.add
Add arguments element-wise.
numpy.cos
Cosine element-wise.
numpy.lib.recfunctions.require_fields
Casts a structured array to a new dtype using assignment by field-name.
numpy.log
Natural logarithm, element-wise.
numpy.mod
Return element-wise remainder of division.
numpy.sin
Trigonometric sine, element-wise.
numpy.tan
Compute tangent element-wise.
numpy.ceil
Return the ceiling of the input, element-wise.
numpy.conj
Return the complex conjugate, element-wise.
numpy.cosh
Hyperbolic cosine, element-wise.
numpy.fabs
Compute the absolute values element-wise.
numpy.fmod
Return the element-wise remainder of division.
numpy.less
Return the truth value of (x1 < x2) element-wise.
numpy.log2
Base-2 logarithm of `x`.
numpy.sign
Returns an element-wise indication of the sign of a number.
numpy.sinh
Hyperbolic sine, element-wise.
numpy.tanh
Compute hyperbolic tangent element-wise.
numpy.equal
Return (x1 == x2) element-wise.
numpy.core._multiarray_umath.datetime_as_string
Convert an array of datetimes into an array of strings.
numpy.floor
Return the floor of the input, element-wise.
numpy.frexp
Decompose the elements of x into mantissa and twos exponent.
numpy.hypot
Given the "legs" of a right triangle, return its hypotenuse.
numpy.isinf
Test element-wise for positive or negative infinity.
numpy.ldexp
Returns x1 * 2**x2, element-wise.
numpy.trunc
Return the truncated value of the input, element-wise.
numpy.arccos
Trigonometric inverse cosine, element-wise.
numpy.arcsin
Inverse sine, element-wise.
numpy.arctan
Trigonometric inverse tangent, element-wise.
numpy.around
Evenly round to the given number of decimals.
numpy.divide
Returns a true division of the inputs, element-wise.
numpy.divmod
Return element-wise quotient and remainder simultaneously.
numpy.source
Print or write to a file the source code for a NumPy object.
numpy.square
Return the element-wise square of the input.
numpy.arccosh
Inverse hyperbolic cosine, element-wise.
numpy.arcsinh
Inverse hyperbolic sine element-wise.
numpy.arctan2
Element-wise arc tangent of ``x1/x2`` choosing the quadrant correctly.
numpy.arctanh
Inverse hyperbolic tangent element-wise.
numpy.deg2rad
Convert angles from degrees to radians.
numpy.degrees
Convert angles from radians to degrees.
numpy.greater
Return the truth value of (x1 > x2) element-wise.
numpy.rad2deg
Convert angles from radians to degrees.
numpy.radians
Convert angles from degrees to radians.
numpy.signbit
Returns element-wise True where signbit is set (less than zero).
numpy.spacing
Return the distance between x and the nearest adjacent number.
numpy.copysign
Change the sign of x1 to that of x2, element-wise.
numpy.diagonal
Return specified diagonals.
numpy.isfinite
Test element-wise for finiteness (not infinity or not Not a Number).
numpy.multiply
Multiply arguments element-wise.
numpy.negative
Numerical negative, element-wise.
numpy.subtract
Subtract arguments, element-wise.
numpy.heaviside
Compute the Heaviside step function.
numpy.logaddexp
Logarithm of the sum of exponentiations of the inputs.
numpy.nextafter
Return the next floating-point value after x1 towards x2, element-wise.
numpy.not_equal
Return (x1 != x2) element-wise.
numpy.left_shift
Shift the bits of an integer to the left.
numpy.less_equal
Return the truth value of (x1 <= x2) element-wise.
numpy.logaddexp2
Logarithm of the sum of exponentiations of the inputs in base-2.
numpy.logical_or
Compute the truth value of x1 OR x2 element-wise.
numpy.nan_to_num
Replace NaN with zero and infinity with large finite numbers (default
numpy.reciprocal
Return the reciprocal of the argument, element-wise.
numpy.bitwise_not
Compute bit-wise inversion, or bit-wise NOT, element-wise.
numpy.einsum_path
Evaluates the lowest cost contraction order for an einsum expression by
numpy.histogram2d
Compute the bi-dimensional histogram of two data samples.
numpy.logical_and
Compute the truth value of x1 AND x2 element-wise.
numpy.logical_not
Compute the truth value of NOT x element-wise.
numpy.logical_xor
Compute the truth value of x1 XOR x2, element-wise.
numpy.right_shift
Shift the bits of an integer to the right.
numpy.ma.abs
Calculate the absolute value element-wise.
numpy.ma.add
Add arguments element-wise.
numpy.ma.cos
Cosine element-wise.
numpy.ma.log
Natural logarithm, element-wise.
numpy.ma.mod
Return element-wise remainder of division.
numpy.floor_divide
Return the largest integer smaller or equal to the division of the inputs.
numpy.ma.sin
Trigonometric sine, element-wise.
numpy.ma.tan
Compute tangent element-wise.
numpy.ma.ceil
Return the ceiling of the input, element-wise.
numpy.ma.cosh
Hyperbolic cosine, element-wise.
numpy.fft.ifft
Compute the one-dimensional inverse discrete Fourier Transform.
numpy.ma.fabs
Compute the absolute values element-wise.
numpy.ma.fmod
Return the element-wise remainder of division.
numpy.ma.less
Return the truth value of (x1 < x2) element-wise.
numpy.ma.log2
Base-2 logarithm of `x`.
numpy.ma.tests.test_subclassing.SubArray
ndarray(shape, dtype=float, buffer=None, offset=0,
numpy.ma.sinh
Hyperbolic sine, element-wise.
numpy.greater_equal
Return the truth value of (x1 >= x2) element-wise.
numpy.ma.tanh
Compute hyperbolic tangent element-wise.
numpy.busdaycalendar
A business day calendar object that efficiently stores information
numpy.fft.ifftn
Compute the N-dimensional inverse discrete Fourier Transform.
numpy.ma.equal
Return (x1 == x2) element-wise.
numpy.ma.floor
Return the floor of the input, element-wise.
numpy.ma.hypot
Given the "legs" of a right triangle, return its hypotenuse.
numpy.ma.arccos
Trigonometric inverse cosine, element-wise.
numpy.ma.arcsin
Inverse sine, element-wise.
numpy.ma.arctan
Trigonometric inverse tangent, element-wise.
numpy.ma.divide
Returns a true division of the inputs, element-wise.
numpy.lib.recfunctions.unstructured_to_structured
Converts an n-D unstructured array into an (n-1)-D structured array.
numpy.ma.arccosh
Inverse hyperbolic cosine, element-wise.
numpy.ma.arcsinh
Inverse hyperbolic sine element-wise.
numpy.ma.arctan2
Element-wise arc tangent of ``x1/x2`` choosing the quadrant correctly.
numpy.ma.arctanh
Inverse hyperbolic tangent element-wise.
numpy.ma.greater
Return the truth value of (x1 > x2) element-wise.
numpy.ma.multiply
Multiply arguments element-wise.
numpy.ma.negative
Numerical negative, element-wise.
numpy.ma.subtract
Subtract arguments, element-wise.
numpy.ma.conjugate
Return the complex conjugate, element-wise.
numpy.ma.not_equal
Return (x1 != x2) element-wise.
numpy.ma.remainder
Return element-wise remainder of division.
numpy.ma.empty_like
empty_like(prototype, dtype=None, order='K', subok=True, shape=None)
numpy.ma.less_equal
Return the truth value of (x1 <= x2) element-wise.
numpy.ma.logical_or
Compute the truth value of x1 OR x2 element-wise.
numpy.ma.logical_and
Compute the truth value of x1 AND x2 element-wise.
numpy.ma.logical_not
Compute the truth value of NOT x element-wise.
numpy.ma.logical_xor
Compute the truth value of x1 XOR x2, element-wise.
numpy.ma.true_divide
Returns a true division of the inputs, element-wise.
numpy.ma.floor_divide
Return the largest integer smaller or equal to the division of the inputs.
numpy.ma.greater_equal
Return the truth value of (x1 >= x2) element-wise.
numpy.core.tests.test_function_base.PhysicalQuantity2
ndarray(shape, dtype=float, buffer=None, offset=0,
numpy.ma.tests.test_subclassing.ComplicatedSubArray
ndarray(shape, dtype=float, buffer=None, offset=0,
numpy.testing._gen_alignment_data
generator producing data with different alignment and offsets
numpy.random.RandomState.rand
Random values in a given shape.
numpy.random.Generator.permuted
Randomly permute `x` along axis `axis`.
np.con*?
Creating Arrays¶
np.arange(10) # similar to MATLAB's 0:9 (and to Python's range())
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.arange(start=1, stop=8, step=3) # MATLAB's 1:3:8
array([1, 4, 7])
np.zeros((2, 3)) # notice that the shape is a tuple
array([[0., 0., 0.],
[0., 0., 0.]])
np.zeros_like(arr_2d)
array([[0, 0, 0],
[0, 0, 0]])
np.ones((1, 4), dtype='int64') # 2-d array with the dtype argument
array([[1, 1, 1, 1]])
np.full((4, 2), 7)
array([[7, 7],
[7, 7],
[7, 7],
[7, 7]])
np.linspace(0, 10, 3) # start, stop, number of points (endpoint as a keyword argument)
array([ 0., 5., 10.])
np.linspace(0, 10, 3, endpoint=False, dtype=np.float32) # float32 is "single" in MATLAB-speak. float64, which is the default, is "double"
array([0. , 3.3333333, 6.6666665], dtype=float32)
np.eye(3, dtype='uint8')
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]], dtype=uint8)
np.diag([19, 20])
array([[19, 0],
[ 0, 20]])
Some more interesting features:
np.array([True, False, False]) # A logical mask
array([ True, False, False])
np.array([1+2j]).dtype # Complex numbers
dtype('complex128')
np.array(['a', 'bc', 'd', 'e'])
# No such thing as a cell array, arrays can contain strings.
array(['a', 'bc', 'd', 'e'], dtype='<U2')
* <U2 are strings containing maximum 2 unicode letters
Arrays can be heterogeneous, although usually this is discouraged.
To make an hetetogeneous array, you have to specify its data type as object, or np.object:
np.array([1, 'b', True, {'b': 1}], dtype=object)
array([1, 'b', True, {'b': 1}], dtype=object)
The last few examples showed us that NumPy arrays are a superset of MATLAB’s matrices, as they also contain the cell array functionality within them.
When multiplying NumPy arrays, multiplication is done cell-by-cell (elementwise), rather than by the rules of linear algebra.
You can still multiply vectors and matrices using one of two options:
The
@operator (preferred):arr1 @ arr2arr1.dot(arr2)
Just remember that the default behavior is different than MATLAB’s.
Note
NumPy does contain a matrix-like array - np.matrix('1 2; 3 4'), which behaves like a linear algebra 2D matrix (see np.matrix), but its use is discouraged.
More on Datatypes¶
While numpy doesn’t require you to actively think of the data type of each of your arrays, it’s a useful habit to have. The existing data types in numpy are:
np.sctypes
{'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64],
'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64],
'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128],
'complex': [numpy.complex64, numpy.complex128, numpy.complex256],
'others': [bool, object, bytes, str, numpy.void]}
Many array creation and handling methods have a dtype keyword argument, that allow you to specify the required output’s data type easily.
Python will issue a RuntimeWarning whenever an “unsafe” conversion of data type will occur, for example from np.float64 to np.float32.
NumPy Arrays vs. Lists¶
You might have asked yourselves by this point what’s the difference between lists and numpy arrays. In other words, if Python already has an array-like data structure, why does it need another one?
Lists are truly amazing, but their flexibility comes at a cost. You won’t notice it when you’re writing some short script, but when you start working with real datasets you notice that their performance is lacking.
Naive iteration over lists is good enough when the lists contain up to a few thousands of elements, but somewhere after this invisible threshold you will start to notice the runtimes of your app turning very slow.
Why are lists slower?¶
Lists are slower due to their implementation. Because a list has to be heterogeneous, a list is actually an object containing references to other objects, which are the elements of the data contained in the list. This nesting can go on even deeper, since elements of lists can be other lists, or other complex data types.
Iterating over such a complicated objects contains a lot of “overhead”, i.e. time the interpreter tries to figure out what is it actually facing - is this current value an integer? A float? A dictionary of tuples?
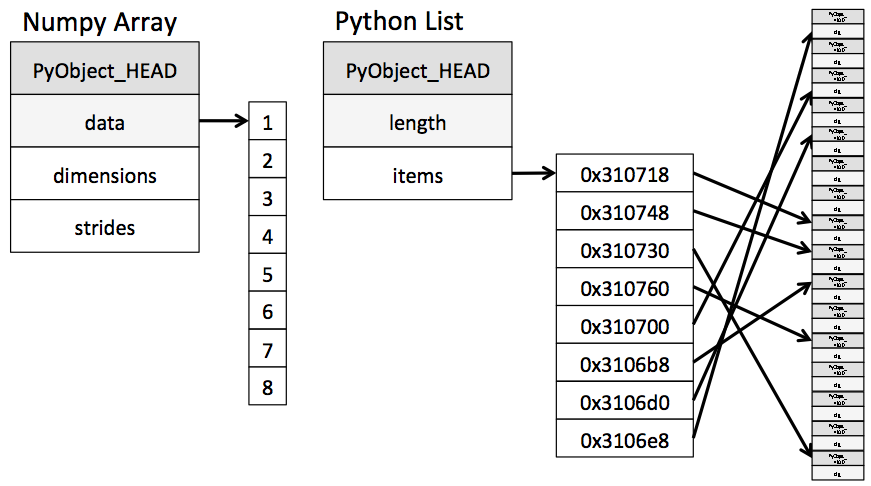
This is where NumPy arrays come into the picture. They require the contained data to be homogeneous (disregarding the “object” datatype), leading to a simpler structure of the underlying implementation: A NumPy array is an object with a pointer to a contiguous block of data in the memory.
NumPy forces the elements in its array to be homogeneous, by means of “upcasting”:
arr = np.array([1, 2, 3.14, 4])
arr # upcasted to float, not "object", since it's much slower
array([1. , 2. , 3.14, 4. ])
This homogeneity and contiguity allows NumPy to use “vectorized” functions, which are simply functions that can iterate in C code over the array, as opposed to regular functions which have to use the Python iteration rules.
This means that while in essence the following two pieces of code are identical, the performance gain is due to the loop being done in C rather than in Python (this is the case in MATLAB as well):
%%timeit
python_array = list(range(1_000_000))
for item in python_array:
item += 1
93.8 ms ± 771 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
%%timeit
numpy_array = np.arange(1_000_000)
numpy_array += 1 # inside, a C loop is adding 1 to each item.
# Two orders of magnitude improvement for a pretty small (1M elements) array.
# This is approximately the size of a 1024x1024 pixel image.
1.14 ms ± 6.29 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
If you recall the first class, you’ll remember that we mentioned how Python code has to be transpiled into C code, which is then compiled to machine code. NumPy arrays take a “shortcut” here, are are quickly compiled to efficient C code without the Python overhead. When using vectorized NumPy operations, the loop Python does in the backstage is very similar to a loop that a C programmer would have written by hand.
Another small but significant benefit of NumPy arrays is smaller memory footprint:
from sys import getsizeof
python_array = list(range(1_000_000))
list_size = getsizeof(python_array) / 1e6 # in MB
print(f"Python list size (1M elements, MB): {list_size}")
numpy_array = np.arange(1_000_000, dtype=np.int32)
numpy_size = numpy_array.nbytes / 1e6
print(f"Numpy array size (1M elements, MB): {numpy_size}")
Python list size (1M elements, MB): 8.000056
Numpy array size (1M elements, MB): 4.0
Why do 1 million elements require 4MB?
Each element has to weigh 4 bytes, or 32 bits. This means that the np.arange() function generates by default int32 values.
Lower memory usage can help us pack larger array in the computer’s working memory (RAM), and it will also improve the performance of the underlying code.
Indexing and Slicing¶
Indexing numpy arrays is very much what you’d expect it to be.
a = np.arange(10)
a[0], a[3], a[-2] # Python indexing is always done with square brackets
(0, 3, 8)
The beautiful reverse slicing works here as well:
a[::-1]
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
arr_2d
array([[1, 2, 3],
[4, 5, 6]])
arr_2d[0, 2] # first row, third column
3
arr_2d[0, :] # first row, all columns
array([1, 2, 3])
arr_2d[0] # first item in the first dimension, and all of its corresponding elemets
# Similar to arr_2d[0, :]
array([1, 2, 3])
a[1::2]
array([1, 3, 5, 7, 9])
a[:2] # last index isn't included
array([0, 1])
View vs. Copy¶
In Python, slicing creates a view of an object, not a copy:
b = a[::2]
b
array([0, 2, 4, 6, 8])
b[0] = 100
b
array([100, 2, 4, 6, 8])
a # a is also changed!
array([100, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Copying is done with copy():
a_copy = a[::-1].copy()
a_copy
array([ 9, 8, 7, 6, 5, 4, 3, 2, 1, 100])
a_copy[1] = 200
a_copy
array([ 9, 200, 7, 6, 5, 4, 3, 2, 1, 100])
a # unchanged
array([100, 1, 2, 3, 4, 5, 6, 7, 8, 9])
This behavior allows NumPy to save time and memory. It will usually go unnoticed during day-to-day use. Occasionally, however, it can result in ugly bugs which are hard to locate.
Let’s look at a summary of 2D indexing:

Aggregation¶
arr = np.random.random(1_000)
sum(arr) # The native Python sum works on numpy arrays, but its use is discouraged in this context
497.76203397015894
sum() is a built-in Python function, capable of working on lists and other native Python data structures. NumPy has its own sum functions: You can either write np.sum(arr), or use arr.sum():
%timeit sum(arr)
%timeit np.sum(arr)
%timeit arr.sum()
98.1 µs ± 413 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
4.83 µs ± 34.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
3.15 µs ± 20.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Keep in mind that the built-in sum() and numpy’s np.sum() aren’t identical. np.sum() by default calculates the sum of all axes, returning a single number for multi-dimensional arrays.
In MATLAB, this behavior is replicated with sum(arr(:)).
Likewise, min() and max() also have two “competing” versions:
%timeit min(arr) # Native Python
%timeit np.min(arr)
%timeit arr.min()
76.4 µs ± 181 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
4.79 µs ± 28.6 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
3.22 µs ± 29.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Calculating the min of an array will, again, result in a single number:
arr2 = np.random.random((4, 4, 4))
arr2.min()
0.004793549617415183
If you wish to calculate it across an axis, use the axis keyword:
arr2.min(axis=0)
array([[0.02993698, 0.10054219, 0.22013973, 0.17841824],
[0.20553447, 0.36647569, 0.16903248, 0.26435175],
[0.13853161, 0.47893816, 0.18592029, 0.21102259],
[0.00479355, 0.14514314, 0.0537409 , 0.44458854]])
2D output (axis number 0 was “dropped”)
arr2.max(axis=(0, 1))
array([0.96677154, 0.81510917, 0.91421898, 0.93054923])
1D output (the two first axes were summed over)
Many other aggregation functions exist, including:
- np.var
- np.std
- np.argmin\argmax
- np.median
- ...
Most of them have an object-oriented version, i.e. arr.var(), and a procedural version, i.e. np.var(arr).
Fancy Indexing¶
In NumPy, indexing an array with a different array is called “fancy” indexing. Perhaps confusingly, it creates a copy, not a view.
basic_array = np.arange(10)
basic_array
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
mask = basic_array % 2 == 0
mask
array([ True, False, True, False, True, False, True, False, True,
False])
b = basic_array[mask] # same as basic_array[basic_array % 2 == 0]
b
array([0, 2, 4, 6, 8])
MATLAB veterans shouldn’t be surprised from this feature, but if you haven’t seen it before make sure to have a firm grasp on it, as it’s a very powerful technique.
b[:] = 999
print(f"basic array: {basic_array}")
print(f"b: {b}")
basic array: [0 1 2 3 4 5 6 7 8 9]
b: [999 999 999 999 999]
Note basic_array was not changed.
float_array = np.arange(start=0, stop=20, step=1.5)
float_array
array([ 0. , 1.5, 3. , 4.5, 6. , 7.5, 9. , 10.5, 12. , 13.5, 15. ,
16.5, 18. , 19.5])
float_array[[1, 2, 5, 5, 10]] # copy, not a view. Meaning that the resulting array is a new
# instance of the original array, independent of it, in a different location in memory.
array([ 1.5, 3. , 7.5, 7.5, 15. ])
Counting the number of values that satisfy some condition can be done using np.count_nonzero() or np.sum():
basic_array = np.arange(10)
count_nonzero_result = np.count_nonzero(basic_array % 2 == 0)
sum_result = np.sum(basic_array % 2 == 0)
print(f"np.count_nonzero result: {count_nonzero_result}")
print(f"np.sum result: {sum_result}")
# In the latter case, True is 1 and False is 0
np.count_nonzero result: 5
np.sum result: 5
If we wish to add more conditions in to the mix, we can use the &, |, ~, ^ operators (and, or, not, xor):
((basic_array % 2 == 1) & (basic_array != 3)).sum() # uneven values that are different from 3
4
Note that numpy uses the &, |, ~, ^ operators for element-by-element comparison, while the reserved and and or keywords evaluate the entire object:
np.sum((basic_array % 2 == 1) and (basic_array != 3)) # doesn't work, "and" isn't used this way here
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-59-e462a6643cbd> in <module>
----> 1 np.sum((basic_array % 2 == 1) and (basic_array != 3)) # doesn't work, "and" isn't used this way here
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
Sorting¶
Again we face a condition in which Python has its own sort functions, but numpy’s np.sort() are much better suited for arrays. We can either sort in-place, or have a new object back:
# Return a new object:
arr = np.array([ 3, 4, 1, 8, 10, 2, 4])
print(np.sort(arr))
# Sort in-place:
arr.sort()
print(arr)
[ 1 2 3 4 4 8 10]
[ 1 2 3 4 4 8 10]
The default implementation is a quicksort but other sorting algorithms can be found as well.
# np.argsort will return the indices of the sorted array:
arr = np.array([ 3, 4, 1, 8, 10, 2, 4])
print("Sorted indices: {}".format(np.argsort(arr)))
# Usage is as follows:
arr[np.argsort(arr)]
Sorted indices: [2 5 0 1 6 3 4]
array([ 1, 2, 3, 4, 4, 8, 10])
Concatenation¶
Concatenation (and splitting) in numpy works as follows:
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
np.concatenate([x, y]) # concatenates along the first axis
array([1, 2, 3, 3, 2, 1])
# Concatenate more than two arrays
z = [99, 99, 99]
np.concatenate([x, y, z]) # notice how the function argument is an iterable!
array([ 1, 2, 3, 3, 2, 1, 99, 99, 99])
# 2D - along the last axis
twod_1 = np.array([[0, 1, 2],
[3, 4, 5]])
twod_2 = np.array([[6, 7, 8],
[9, 10, 11]])
np.concatenate((twod_1, twod_2), axis=-1)
array([[ 0, 1, 2, 6, 7, 8],
[ 3, 4, 5, 9, 10, 11]])
np.vstack() and np.hstack() are also an option:
sim1 = np.array([0, 1, 2])
sim2 = np.array([[30, 40, 50],
[60, 70, 80]])
np.vstack((sim1, sim2))
array([[ 0, 1, 2],
[30, 40, 50],
[60, 70, 80]])
Splitting up arrays is also quite easy:
arr = np.arange(16).reshape((4, 4)) # see the tuple? Shapes of arrays always come in tuples
arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
upper, lower = np.split(arr, [3]) # splits at the fourth line (of the first axis, by default)
print(upper)
print('---')
print(lower)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
---
[[12 13 14 15]]
Familiarization Exercise
Create two random 3D arrays, at least 3x3x3 in size. The first should have random integers between 0 and 100, while the second should contain floating points numbers drawn from the normal distribution, with mean -1 and standard deviation of 2
What are the default datatypes of integer and floating-point arrays in NumPy?
Solution
>>> low = 0
>>> high = 100
>>> size = 10, 10, 10
>>> array_1 = np.random.randint(low=low, high=high, size=size)
>>> array_2 = np.random.randn(*size) * 2 - 1
>>> array_1.dtype
dtype('int64')
>>> array_2.dtype
dtype('float64')
Center the distribution of the first integer array around 0, with minimal and maximal values ranging between -1 and 1.
Solution
>>> middle = (array_1.max() - array_1.min()) / 2
>>> centered_array_1 = (array_1 - middle) / middle
Calculate the mean and standard deviation of each array along the last axis, and the sum along the second axis. Use the object-oriented implementation of these functions.
Solution
>>> print("\narray_1 (integers) stats:")
>>> print(f"Mean:\t{array_1.mean()}\nSTD:\n{array_1.std(axis=-1)}\nSum:\n{array_1.sum(axis=1)}")
>>> print("\narray_2 (normal distribution) stats:")
>>> print(f"Mean:\t{array_2.mean()}\nSTD:\n{array_2.std(axis=-1)}\nSum:\n{array_2.sum(axis=1)}")
array_1 (integers) stats:
Mean: 49.025,
STD:
[[27.78920654 29.11717706 20.05218193 32.00312485 26.01326585 29.29573348
25.86909353 28.75499957 34.52375993 24.20826305]
[30.57384503 21.83689538 27.17149241 25.25787006 35.64112793 21.12912682
14.4374513 23.75731466 29.45318319 31.1409698 ]
[25.87063973 20.33445352 18.49432345 31.76727876 32.89924011 26.18320072
28.70261312 31.11414469 25.03118056 30.24053571]
[25.84202004 25.30138336 26.71048483 26.84399374 34.29518917 24.79516082
33.25793138 24.05826261 28.38309356 22.46241305]
[32.46921619 26.38181192 27.77426867 30.57515331 17.3104015 28.16398409
29.29573348 30.30923952 28.85896741 31.8127333 ]
[29.20291081 23.5246679 30.04063914 33.97072269 32.72002445 36.88482073
23.46060528 38.49792202 24.27838545 31.66954373]
[31.11976864 26.27717641 26.91635191 27.3086067 25.55875584 30.85919636
31.20272424 15.94647296 27.45614685 25.2031744 ]
[28.02231254 16.16817862 24.10311183 24.19586742 30.42696173 29.29436806
22.29798197 11.81905242 32.83671725 29.80083891]
[30.95545186 23.54761134 24.0840196 25.76994373 20.41568025 30.13370206
25.76121115 17.87064632 28.63145124 25.72722294]
[28.33372549 36.33455655 27.97570374 19.85849944 32.28374204 30.42383934
31.57277308 29.06819568 30.36774605 21.08198283]]
Sum:
[[389 628 553 626 422 450 465 530 446 341]
[580 487 494 408 595 601 532 344 425 549]
[499 548 450 584 470 516 439 370 630 552]
[461 373 472 534 657 484 521 409 497 557]
[559 329 516 486 453 549 577 632 610 533]
[326 573 492 411 341 659 534 538 523 406]
[499 342 567 404 306 550 445 590 526 383]
[428 615 495 447 559 628 602 543 470 560]
[594 410 526 410 469 444 468 454 482 488]
[382 432 427 560 456 525 437 435 290 442]]
array_2 (normal distribution) stats:
Mean: -1.07406427297348
STD:
[[1.9062669 1.35123452 2.28887043 3.19893326 1.77835265 2.11393339
1.97726446 1.80244267 1.52636428 2.31044054]
[1.73597656 1.71712516 1.47350922 2.27424207 1.89264104 1.47622583
1.68845783 1.80765036 1.69611444 1.16962201]
[2.01873356 2.41661259 1.18562369 2.09256735 1.95677542 1.99870136
1.50354672 1.71964295 2.34980052 1.94775582]
[2.2962578 1.87748841 1.89627904 1.45126248 1.89634329 2.6596314
1.78224436 1.42400012 2.4198374 1.10558226]
[1.54355846 2.1550968 2.11254107 1.49251463 2.65904808 1.76607792
2.28877444 2.48845674 1.97714146 1.93987525]
[2.36294492 1.29003435 1.67418127 2.01515922 2.55921084 1.70214685
1.61930304 1.66534386 1.24618498 1.67461576]
[1.96178897 1.9084264 1.54803035 2.16445385 1.98760056 1.62776124
1.39459135 1.56244261 1.56990164 1.04599902]
[2.03492831 2.05964846 2.05118908 2.02421875 0.9999559 1.49058598
1.57629449 2.39801109 1.59726342 2.23059835]
[2.00656501 2.12156103 1.27455901 1.39537464 1.5390344 2.53181591
1.54110338 1.04873726 1.42964864 1.99864807]
[2.20401184 2.1256408 1.27375107 1.97627528 2.15301994 1.98771765
1.34703697 1.84095639 2.44256394 1.86033268]]
Sum:
[[ -3.69494856 -16.42937164 -6.43041941 -15.79987592 -15.07933552
-2.87887616 -6.21164117 -1.17030658 -16.98166317 -8.33184059]
[ -8.31375346 -10.01798326 -4.53252787 -6.75151056 -12.59403445
-15.03168533 -15.00973464 -16.74814014 -7.51746325 -5.06873569]
[ -6.21037079 -12.48702723 -13.36792767 -13.62958844 -18.88755083
-16.0526574 -2.96677257 -3.60762824 -9.48245148 -2.25873247]
[ -9.44142793 -10.94941452 -12.60956367 -14.14565696 -11.40547929
-21.41164387 -15.442485 -12.67828496 -14.61969791 -18.65552896]
[-23.74338934 -15.62870646 -5.87073755 -2.67523936 -7.02999193
-16.09719664 -22.51205356 -6.49143903 -25.33126019 -6.98015729]
[-14.05676394 -13.55744558 -11.09719127 -16.75825685 -14.63107293
-6.38490618 -12.71933776 -10.89879605 -13.34727072 -15.67801212]
[-21.04560354 -4.8036513 0.8706029 -8.04820513 -4.97612456
-16.2730379 -11.00863391 -13.07748112 -14.63053689 -10.53706972]
[-11.405159 -6.737532 -13.7992876 -5.08953287 -11.33180152
-12.02206524 -9.687376 -18.24794133 -16.52195639 -8.70169963]
[ -6.41657342 -5.77920315 1.49536367 -5.43976838 -7.37647914
-2.6746939 -11.93431435 -13.04875607 -10.88735467 -22.83205649]
[-17.77186949 -0.24316503 -3.39047633 -9.0471082 -5.90565106
-15.32306311 -0.57743855 -1.7062542 -11.35829268 -10.38006335]]
Iteration Exercise
Find and return the indices of the two random arrays only where both elements satisfy -0.5 <= value <= 0.5. Do so in at least two distinct ways. These can include element-wise iteration, masked-arrays, and more.
Time the execution of the script using the IPython %%timeit magic if you have this tool near at hand.
Solution
Using element-wise iteration:
>>> %%timeit
>>> values = zip(array_1.flat, array_2.flat)
>>> result = []
>>> for index, (value_1, value_2) in enumerate(values):
>>> if (-0.5 <= value_1 <= 0.5) and (-0.5 <= value_2 <= 0.5):
>>> result.append(index)
>>> result
4.55 ms ± 150 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Using a mask:
>>> %%timeit
>>> mask_1 = (-0.5 <= array_1.ravel()) & (array_1.ravel() <= 0.5)
>>> mask_2 = (-0.5 <= array_2.ravel()) & (array_2.ravel() <= 0.5)
>>> both = mask_1 & mask_2
>>> result = np.where(both)
>>> result
16.3 µs ± 236 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
Broadcasting Exercise
Create a vector with length 100, filled with ones, and a 2D zero-filled array with its last dimension with size of 100.
Solution
>>> vec = np.ones(100)
>>> mat = np.zeros((10, 100))
Using
np.tile(), add the vector and the array.
Solution
>>> tiled_vec = np.tile(vec, (10, 1))
>>> ans_tiled = mat + tiled_vec
Did you have to use
np.tile()in this case? What feature ofnumpyallows this?
Solution
Array broadcasting enables the same behavior:
>>> ans_simple = mat + vec
What happens to the non-tiled addition when the first dimension of the matrix is 100? Why?
Solution
>>> mat_transposed = mat.T
>>> print(mat_transposed.shape)
(100, 10)
>>> ans_trans = mat_transposed + vec
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-42-d2a177183ebb> in <module>
----> 1 ans_trans = mat_transposed + vec
ValueError: operands could not be broadcast together with shapes (100,10) (100,)
Broadcasting is done over the last dimension.
Bonus: How can one add the matrix (in its new shape) and vector without
np.tile()?
Solution
>>> ans_newaxis = mat_transposed + vec[:, np.newaxis]
