Contents

Exercise V: Regularization

More information about the dataset can be found here.

This exercise is an adaptation of lab 2 from the ISLR, in which the salary of baseball players is predicted on the basis of various statistics associated with performance in the previous year.

Set up

import pandas as pd

URL = "https://raw.githubusercontent.com/JWarmenhoven/ISLR-python/master/Notebooks/Data/Hitters.csv"
data = pd.read_csv(URL, index_col=0)

General Inspection and Preprocessing

data
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks League Division PutOuts Assists Errors Salary NewLeague
-Andy Allanson 293 66 1 30 29 14 1 293 66 1 30 29 14 A E 446 33 20 NaN A
-Alan Ashby 315 81 7 24 38 39 14 3449 835 69 321 414 375 N W 632 43 10 475.0 N
-Alvin Davis 479 130 18 66 72 76 3 1624 457 63 224 266 263 A W 880 82 14 480.0 A
-Andre Dawson 496 141 20 65 78 37 11 5628 1575 225 828 838 354 N E 200 11 3 500.0 N
-Andres Galarraga 321 87 10 39 42 30 2 396 101 12 48 46 33 N E 805 40 4 91.5 N
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
-Willie McGee 497 127 7 65 48 37 5 2703 806 32 379 311 138 N E 325 9 3 700.0 N
-Willie Randolph 492 136 5 76 50 94 12 5511 1511 39 897 451 875 A E 313 381 20 875.0 A
-Wayne Tolleson 475 126 3 61 43 52 6 1700 433 7 217 93 146 A W 37 113 7 385.0 A
-Willie Upshaw 573 144 9 85 60 78 8 3198 857 97 470 420 332 A E 1314 131 12 960.0 A
-Willie Wilson 631 170 9 77 44 31 11 4908 1457 30 775 357 249 A W 408 4 3 1000.0 A

322 rows × 20 columns

Well, it looks like a dataset.

Let’s probe a little deeper:

data.info()

<class 'pandas.core.frame.DataFrame'>
Index: 322 entries, -Andy Allanson to -Willie Wilson
Data columns (total 20 columns):
 #   Column     Non-Null Count  Dtype  
---  ------     --------------  -----  
 0   AtBat      322 non-null    int64  
 1   Hits       322 non-null    int64  
 2   HmRun      322 non-null    int64  
 3   Runs       322 non-null    int64  
 4   RBI        322 non-null    int64  
 5   Walks      322 non-null    int64  
 6   Years      322 non-null    int64  
 7   CAtBat     322 non-null    int64  
 8   CHits      322 non-null    int64  
 9   CHmRun     322 non-null    int64  
 10  CRuns      322 non-null    int64  
 11  CRBI       322 non-null    int64  
 12  CWalks     322 non-null    int64  
 13  League     322 non-null    object 
 14  Division   322 non-null    object 
 15  PutOuts    322 non-null    int64  
 16  Assists    322 non-null    int64  
 17  Errors     322 non-null    int64  
 18  Salary     263 non-null    float64
 19  NewLeague  322 non-null    object 
dtypes: float64(1), int64(16), object(3)
memory usage: 52.8+ KB

Calling info() reveals that most (16/19) columns contain integers, except for Salary which is a float and League, NewLeague, and Division which are object (categorical). Even more importantly, it shows that Salary contains missing observations. Because Salary is our target variable, we don’t really have any use for these observations and would be better off simply dropping them from our dataset:

data.dropna(subset=["Salary"], inplace=True)

Done.

Next, we might give describe() a quick look:

pd.set_option('float_format', '{:.4g}'.format)
data.describe()
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks PutOuts Assists Errors Salary
count 263 263 263 263 263 263 263 263 263 263 263 263 263 263 263 263 263
mean 403.6 107.8 11.62 54.75 51.49 41.11 7.312 2658 722.2 69.24 361.2 330.4 260.3 290.7 118.8 8.593 535.9
std 147.3 45.13 8.757 25.54 25.88 21.72 4.794 2287 648.2 82.2 331.2 323.4 264.1 279.9 145.1 6.607 451.1
min 19 1 0 0 0 0 1 19 4 0 2 3 1 0 0 0 67.5
25% 282.5 71.5 5 33.5 30 23 4 842.5 212 15 105.5 95 71 113.5 8 3 190
50% 413 103 9 52 47 37 6 1931 516 40 250 230 174 224 45 7 425
75% 526 141.5 18 73 71 57 10 3890 1054 92.5 497.5 424.5 328.5 322.5 192 13 750
max 687 238 40 130 121 105 24 1.405e+04 4256 548 2165 1659 1566 1377 492 32 2460

Scaling

I seems like there’s fairly large variabiliy in scale between the different features, and in any case regularization requires some form of standardization.

First, let’s differntiate the features matrix (X) from the target vector (y):

target_name = "Salary"

X = data.drop(columns=[target_name])
y = data[target_name].copy()

Only numeric columns should be standardized, so let’s also be sure to distinguish those from the categoricals:

numeric_features = X.select_dtypes([int, float])

And we’re all set:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X.loc[:, numeric_features.columns] = scaler.fit_transform(
    X.loc[:, numeric_features.columns])

X
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks League Division PutOuts Assists Errors NewLeague
-Alan Ashby -0.6029 -0.5957 -0.5286 -1.206 -0.5221 -0.09753 1.398 0.3468 0.1744 -0.00292 -0.1217 0.259 0.4353 N W 1.221 -0.5232 0.2134 N
-Alvin Davis 0.5125 0.4923 0.73 0.4415 0.7941 1.609 -0.9012 -0.4529 -0.4099 -0.07605 -0.4151 -0.1996 0.01037 A W 2.109 -0.2539 0.82 A
-Andre Dawson 0.6282 0.7365 0.9588 0.4023 1.026 -0.1898 0.7709 1.302 1.318 1.899 1.412 1.573 0.3557 N E -0.3247 -0.7442 -0.8482 N
-Andres Galarraga -0.5621 -0.4625 -0.1853 -0.6177 -0.3672 -0.5127 -1.11 -0.9909 -0.9602 -0.6977 -0.9475 -0.8812 -0.8623 N E 1.841 -0.5439 -0.6966 N
-Alfredo Griffin 1.295 1.358 -0.8718 0.7553 -0.01884 -0.2821 0.7709 0.767 0.635 -0.6124 0.4228 0.01729 -0.2514 A W -0.03118 2.087 2.488 A
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
-Willie McGee 0.635 0.4257 -0.5286 0.4023 -0.135 -0.1898 -0.4832 0.01992 0.1295 -0.4539 0.05378 -0.06016 -0.4639 N E 0.1227 -0.758 -0.8482 N
-Willie Randolph 0.601 0.6255 -0.7574 0.8338 -0.05755 2.44 0.9799 1.25 1.219 -0.3686 1.621 0.3736 2.332 A E 0.07977 1.811 1.73 A
-Wayne Tolleson 0.4853 0.4034 -0.9862 0.2454 -0.3285 0.5022 -0.2742 -0.4196 -0.447 -0.7586 -0.4363 -0.7356 -0.4336 A W -0.9081 -0.03978 -0.2416 A
-Willie Upshaw 1.152 0.8031 -0.2997 1.187 0.3295 1.702 0.1438 0.2368 0.2084 0.3384 0.3291 0.2776 0.2722 A E 3.662 0.08452 0.5167 A
-Willie Wilson 1.546 1.38 -0.2997 0.873 -0.2898 -0.4666 0.7709 0.9861 1.136 -0.4783 1.252 0.08236 -0.04275 A W 0.4198 -0.7925 -0.8482 A

263 rows × 19 columns

X.describe()
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks PutOuts Assists Errors
count 263 263 263 263 263 263 263 263 263 263 263 263 263 263 263 263
mean 1.013e-17 5.741e-17 3.377e-17 -5.066e-17 1.216e-16 1.689e-18 -5.403e-17 6.079e-17 6.754e-17 5.403e-17 3.377e-17 4.053e-17 1.081e-16 7.43e-17 0 1.047e-16
std 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002 1.002
min -2.616 -2.372 -1.329 -2.148 -1.993 -1.897 -1.319 -1.156 -1.11 -0.844 -1.087 -1.014 -0.9837 -1.04 -0.8201 -1.303
25% -0.8239 -0.8066 -0.7574 -0.8334 -0.8317 -0.8356 -0.6922 -0.7953 -0.7886 -0.6611 -0.7736 -0.7294 -0.7181 -0.6343 -0.7649 -0.8482
50% 0.06364 -0.1072 -0.2997 -0.1077 -0.1737 -0.1898 -0.2742 -0.3183 -0.3187 -0.3564 -0.3365 -0.3111 -0.3273 -0.2388 -0.5094 -0.2416
75% 0.8322 0.7476 0.73 0.7161 0.7554 0.7329 0.5619 0.5402 0.5129 0.2835 0.4123 0.2915 0.2589 0.1138 0.5058 0.6683
max 1.927 2.89 3.247 2.952 2.691 2.947 3.488 4.993 5.462 5.836 5.457 4.116 4.954 3.888 2.578 3.55

Warning

Try to consider the way in which standardization was applied. Can you think of anything that could pose a problem in following steps?

Solution

Applying standardization prior to the train-test split results in information (mean and standard deviation) from the test set “leaking” into the training set, and therefore should be avoided! The correct procedure is to apply standardization separately after splitting the data.

Pairwise Scatter-matrix

_ = pd.plotting.scatter_matrix(data, figsize=(15, 15))
../../_images/exercise_05_26_0.png

Dummy Encoding

To view the different values each categorical variable holds:

for feature in X.select_dtypes(object):
    print(feature.ljust(10), X[feature].unique())

League     ['N' 'A']
Division   ['W' 'E']
NewLeague  ['N' 'A']

And to “dummy encode” it is as simple as:

X = pd.get_dummies(X, drop_first=True)

X.sample(20).select_dtypes(include=["uint8"]).style.background_gradient()
  League_N Division_W NewLeague_N
-Ken Landreaux 1 1 1
-Ron Hassey 0 0 0
-Shawon Dunston 1 0 1
-Chris Bando 0 0 0
-Don Mattingly 0 0 0
-Ken Phelps 0 1 0
-Gary Carter 1 0 1
-Al Newman 1 0 0
-Rick Dempsey 0 0 0
-Wally Joyner 0 1 0
-Kevin Bass 1 1 1
-Leon Durham 1 0 1
-Jesse Barfield 0 0 0
-Brian Downing 0 1 0
-Tom Brunansky 0 1 0
-Terry Kennedy 1 1 0
-Jody Davis 1 0 1
-Dwight Evans 0 0 0
-Argenis Salazar 0 1 0
-Ted Simmons 1 1 1

Model Creation

In the previous linear regression exercise we used sklearn’s LinearRegression class along with the train_test_split() function to model the relationship between the features and the target variable and evaluate it’s performance in predicting the target variable for an out-of-sample collection of observations. In this exercise, we will use LassoCV and RidgeCV to introduce the \(\ell_1\) and \(\ell_2\) penalties as part of our fitting process and regularize the coefficients of our predictors. In addition, cross-validation will also be taken care of automatically.

For the sake of uniformity we’ll use the same list of regularization parameter values:

import numpy as np

alphas = np.linspace(0.01, 100, 200)

Lasso (\(\ell_1\))

from sklearn.linear_model import LassoCV

lasso_model = LassoCV(alphas=alphas, max_iter=10000)
_ = lasso_model.fit(X, y)

Ridge (\(\ell_2\))

from sklearn.linear_model import RidgeCV

ridge_model = RidgeCV(alphas=alphas, store_cv_values=True)
_ = ridge_model.fit(X, y)

Note

By default, LassoCV will use 5-fold cross-validation with \(R^2\) as the scoring method and RidgeCV will use Generalized Cross-Validation, which is a form of efficient Leave-One-Out cross-validation, with negative mean squared error.

To change the splitting strategy, set the cv keyword argument to the number of folds you’d like to use, to specify scoring and other search parameters see the GridSearchCV class.

Model Application

To calculate the predicted salary of each player using the model:

Lasso (\(\ell_1\))

lasso_predictions = lasso_model.predict(X)

Ridge (\(\ell_2\))

ridge_predictions = ridge_model.predict(X)

Model Evaluation

import matplotlib.pyplot as plt


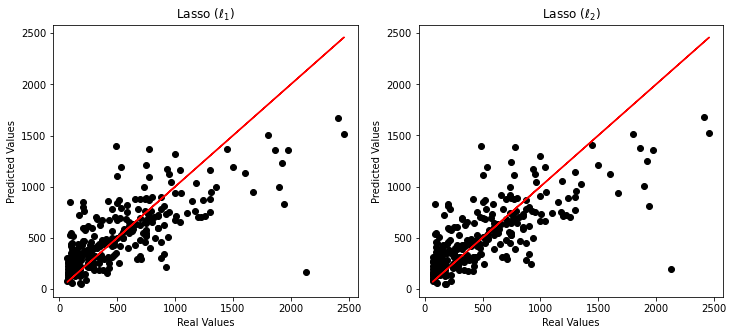
def plot_predictions(y: pd.Series, predictions: pd.Series, ax: plt.Axes):
    ax.scatter(y, predictions, color="black")
    ax.plot(y, y, color="red")
    ax.set_xlabel("Real Values")
    ax.set_ylabel("Predicted Values")


fig, ax = plt.subplots(ncols=2, figsize=(12, 5))
plot_predictions(y, lasso_predictions, ax[0])
ax[0].set_title(r"Lasso ($\ell_1$)")
plot_predictions(y, ridge_predictions, ax[1])
_ = ax[1].set_title(r"Lasso ($\ell_2$)")
../../_images/exercise_05_46_0.png

Alpha

Lasso (\(\ell_1\))

lasso_model.alpha_

2.522311557788944

Ridge (\(\ell_2\))

ridge_model.alpha_

3.527236180904522

Coefficients

coefficients_dict = {"Lasso": lasso_model.coef_, "Ridge": ridge_model.coef_}
coefficients = pd.DataFrame(coefficients_dict, index=X.columns)
coefficients.T
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks PutOuts Assists Errors League_N Division_W NewLeague_N
Lasso -237.2 261.6 0 -0 0 104.8 -46.64 -0 0 44.29 224.5 123.9 -144.8 76.81 26.48 -13.56 27.04 -114.1 0
Ridge -216.4 230.7 0.9447 0.7865 6.002 106.3 -51.34 -94.18 119.4 58.18 199.9 114.5 -144.5 77.68 39.18 -24.86 50.73 -118.6 -18.02 
from sklearn.linear_model import Lasso, Ridge


coef_fig, coef_ax = plt.subplots(ncols=2, figsize=(14, 6))

#########
# Lasso #
#########

simple_lasso = Lasso(max_iter=10_000)
lasso_coefficient_values = []
lasso_alphas = lasso_model.alphas_[::-1]

for alpha in lasso_alphas:
    simple_lasso.set_params(alpha=alpha)
    simple_lasso.fit(X, y)
    lasso_coefficient_values.append(simple_lasso.coef_)

# Coefficient values by alpha
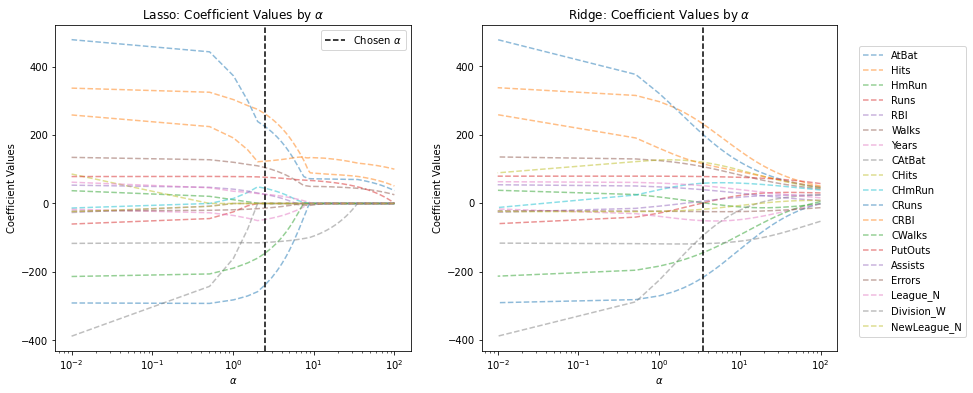
coef_ax[0].semilogx(lasso_alphas, lasso_coefficient_values, linestyle="dashed", alpha=0.5)

# Chosen alpha
coef_ax[0].axvline(lasso_model.alpha_,
                  linestyle='--',
                  color="black",
                  label=r"Chosen $\alpha$")
coef_ax[0].legend()
coef_ax[0].set_xlabel(r'$\alpha$')
coef_ax[0].set_ylabel("Coefficient Values")
coef_ax[0].set_title(r"Lasso: Coefficient Values by $\alpha$")

#########
# Ridge #
#########

simple_ridge = Ridge()
ridge_coefficient_values = []
ridge_alphas = ridge_model.alphas[::-1]

for alpha in ridge_alphas:
    simple_ridge.set_params(alpha=alpha)
    simple_ridge.fit(X, y)
    ridge_coefficient_values.append(simple_ridge.coef_)


# Coefficient values by alpha
coef_ax[1].semilogx(ridge_alphas,
                   ridge_coefficient_values,
                   linestyle="dashed",
                   alpha=0.5)
# Chosen alpha
coef_ax[1].axvline(ridge_model.alpha_,
                  linestyle='--',
                  color="black",
                  label=r"Chosen $\alpha$")
coef_ax[1].legend(X.columns, loc="upper left", bbox_to_anchor=(1.05, 0.95))
coef_ax[1].set_xlabel(r'$\alpha$')
coef_ax[1].set_ylabel("Coefficient Values")
_ = coef_ax[1].set_title(r"Ridge: Coefficient Values by $\alpha$")
../../_images/exercise_05_53_0.png

Mean Squared Error (MSE)

mse_fig, mse_ax = plt.subplots(ncols=2, figsize=(14, 6))

#########
# Lasso #
#########

lasso_alphas = lasso_model.alphas_
lasso_mse = lasso_model.mse_path_

# Cross-validation MSEs
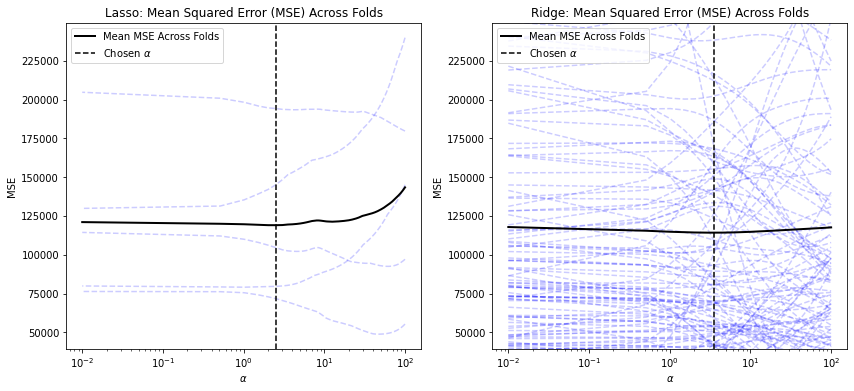
mse_ax[0].semilogx(lasso_alphas,
                   lasso_mse,
                   linestyle="dashed",
                   color="blue",
                   alpha=0.2)

# Mean MSE
mse_ax[0].plot(lasso_alphas,
               lasso_mse.mean(axis=-1),
               color="black",
               label="Mean MSE Across Folds",
               linewidth=2)
# Chosen alpha
mse_ax[0].axvline(lasso_model.alpha_,
                  linestyle='--',
                  color="black",
                  label=r"Chosen $\alpha$")
mse_ax[0].legend()
mse_ax[0].set_xlabel(r'$\alpha$')
mse_ax[0].set_ylabel("MSE")
mse_ax[0].set_title("Lasso: Mean Squared Error (MSE) Across Folds")

#########
# Ridge #
#########

ridge_alphas = ridge_model.alphas
ridge_mse = ridge_model.cv_values_.T

# Cross-validation MSEs
mse_ax[1].semilogx(ridge_alphas,
                   ridge_mse,
                   linestyle="dashed",
                   color="blue",
                   alpha=0.2)
# Mean MSE
mse_ax[1].plot(ridge_alphas,
               ridge_mse.mean(axis=-1),
               color="black",
               label="Mean MSE Across Folds",
               linewidth=2)
# Chosen alpha
mse_ax[1].axvline(ridge_model.alpha_,
                  linestyle='--',
                  color="black",
                  label=r"Chosen $\alpha$")
mse_ax[1].legend()
mse_ax[1].set_xlabel(r'$\alpha$')
mse_ax[1].set_ylabel("MSE")
mse_ax[1].ticklabel_format(style="plain", axis="y")
mse_ax[1].set_ylim(mse_ax[0].get_ylim())
_ = mse_ax[1].set_title("Ridge: Mean Squared Error (MSE) Across Folds")
../../_images/exercise_05_55_0.png

\(R^2\)

To calculate in-sample \(R^2\) score for each model:

Lasso (\(\ell_1\))

lasso_model.score(X, y)

0.5342574616741457

Ridge (\(\ell_2\))

ridge_model.score(X, y)

0.5364706351171298

Note that calculating in-sample \(R^2\) scores will result in underestimating prediction error.

Note

For a more generalized solution for parameter tuning, see sklearn’s GridSearchCV.

previous

Exercise IV: Logistic Regression

next

Exercise VI: Revisiting Linear and Logistic Regression